ランキング「関数」わかりました！(63125,5)

10月7日の日記以来，さらにデータがたまりましたので，またちょっとエクセルで遊びます．かなり長くなるので，数学（数式・グラフ）の嫌いな方は，最後の結論だけ見てください．

今までは，

１）ランキングは，過去１週間の訪問者数で決まる．ただし，この値は，一般参加者の我々にはわからない．
２）他方，我々には，100名訪問者が増える毎に通知がリアルタイ ムで来る．前回の通知日時と引き算すれば，100名増えるのに要した時間がわかることになる．
3)100名増えるのに要する時間が長いほど，１週間の訪 問者数は減るから，ランキングは落ちる．したがって，100名増えるのに要する時間とランキングとは相関関係がある．

ということから，ランキングと100名増えるのに要する時間（日数）を比較していましたが，訪問者数が増えてくると，2)のデータから毎日の0時の時点での訪問者数が精度よく推定できるので，１週間の訪問者数がわかります．それで，推定した1週間の訪問者数とランキングの関係を描いたのが上の図です．データを取り始めた今年の2月11日から10月31日までの93個のデータを使っています．訪問者数が増えると直線状にランキングが上がって（グラフ上では点が下がって）行きますが，徐々に訪問者数が増える割にはランキングが上がらなくなります．まあ，直感的も納得できる結果ですね．この形は，理工系研究者の大好きな指数関数的な形をしているので，早速指数関数で近似してみます．

予想通り，非常にきれいに指数関数で近似できることがわかりました．式はy = 185.13exp(-0.0047x)となります．ここでy=ランキング，x＝１週間の（推定）訪問者数です．これを逆にとくと，x=1111-213lｎ(y)となります．ln(y)はｙの自然対数です．これによって，ランキングから１週間の訪問者数を計算することができます．ランキング50位なら延べ約280名，20位なら約470名，10位なら約620名となります．さらに，ランキング一位なら1111名となりますが，一位ともなると話はさらに厳しくなります．このグラフのY軸を対数にしてみましょう．

指数関数はこのようにY軸のみを対数にすると直線になるはずです．確かにランキング10位くらいまでは直線に載りますが，それより以下では右横の方に（訪問者数が増えるほうに）点がずれています．上記の指数関数はこのグラフ上では直線になっており，それを延長してランキング一位のところに持ってくると，確かに1100名くらいのところに来ていますが，点の分布を見る限り，それよりは右（人数の増える方）に来そうなことがわかります．それでｘ軸（訪問者数）の方も対数にして両対数で見てみることにします．

両対数で見てみると，特にランキング10位以下では，こちらの方が直線に載ってくる感じです．もっとも，「両対数でグラフを書くとたいていのものが直線関係に見える」ということがあるので，それには注意が必要ですが，とりあえずこの「直線」関係を信ずると，ｙはｘの指数関数ではなくｘのべき乗の形になります．このグラフ上でべき乗関数をあてはめてやると

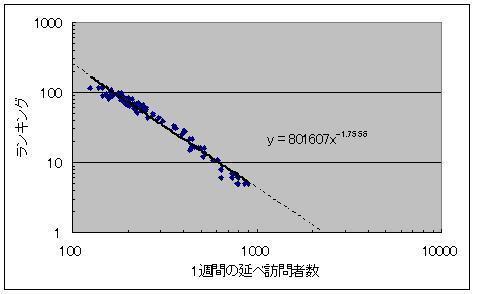
上のようなグラフになります．式はy = 801607x^(-1.7556) （ｘの-1.7556乗）ですね．これからｘを出すとｘ＝2306y^(-0.57)となり，ｙ＝1（ランキング１位）のとき，ｘ（１週間訪問者数）＝2306名となります．上のグラフでも直線を延長すると，ｙ＝１のときｘが二千数百になっていることがわかります．

以上をまとめると,y:ランキング，x：過去１週間の延べ訪問者数としたとき，ｙはｘの指数関数またはべき乗であらわされ，

ｙ＝185.13exp(-0.0047x)，x=1111- 213lｎ(y)でy=1のときx=1111
または
y = 801607x^(-1.7556) ,ｘ＝2306y^(-0.57)でｙ=１のときx=2306

です．